5 Sorting Algorithms Every Programmer Should Know | Sorting Methods

 Sorting Methods :

1.  Bubble Sort :

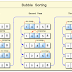
1. In this sorting method, the list is divided into tow sub-list sorted an unsorted. The smallest element is  bubbled from unsorted sub-list. After moving the smallest element the imaginary will moves one element ahead.
2. The bubble sort was originally written to bubble up the highest element in the list. But there is no difference whether highest / lowest element is bubbled.
3. This method is easy to understand but time consuming. In this type, two successive elements are compared and swapping is done. Thus, step-by-step entire array elements are checked. Given a list of ‘n’ elements that bubble sort requires up to n-1 passes to sort the data.
4. To arrange the elements in the ascending order, we compare each item in the list with the item next to it and swapping them if required. The algorithm repeats these comparison process until n-1 passes where n is the number of input items. For ‘sink’ towards the beginning of the list.
5. Suppose, the list of number A[0], A[1], A[2],---A[n-1] is in memory, which is to be sorted.

Algorithm

Step 1 :  Read N, number of elements in the list

Step 2 : Read Array A[0], A[1]---A[n-1]

Step 3 : For I =0 to N-1 do

                For j=0 to N-i-1 do

                If(A[j]>A[j+1] ) then

                Temp=A[j]

                A[j]=A[j+1]

    A[j+1]=temp

Step 4: Stop

 

Insertion Sort :

1. In insertion sort the element is inserted at an appropriate place. Here the array divided into two parts sorted and unsorted sub-array is picked up and moved into the sorted sub array by inserting in suitable position.
2. Relatively simple and easy to implement .
3. Inefficient for large array as time complexity in O(n2).
4. The insertion sort is highly efficient if the array is already in almost sorted order.

Algorithm :

Step 1 : Set I =1;

Step 2 : key A[i];

Step 3 : Set j=i-1;

Step 4 : If key<A[j]then

                 A[j+1] =A[j];

    J=j-1;

    Repeat step 2 until j>=0;

Step 5 :   A[j+1] = key;

                I=i+1;

Step 6 :  Repeat step from 2 to 5 till i<N

Step 7 :  Stop

 

Quick Sort :

1. It is more popular and fastest sorting method.
2. If follows divide and conquer method i.e. numbers are divided and again subdivided and division goes on until it is not possible to divide further the procedure is applied recursively to the two parts of the array, on either side of the pivot element. It is also called partition-exchange sort.
3. This algorithm divides the input list into three main parts :
4. Elements less than the pivot element.
5. Pivot element(Central element).
6. Elements greater than the pivot element.
7. Pivot element can be any element form the array, it can be the first element, the last element or any random element.
8. Recursive Algorithm consists of four steps.
9. If There is one or less element in the array to be sorted, return immediately.
10. Pick an element in the array to serve as a “Pivot”  element,(Usually, the left most element in the array)
11. Split the array into two parts one with elements smaller than the pivot and the other with elements larger than the pivot.
12. Recursively repeat the algorithm for both halves of the original array.

 Algorithm :

Step 1 : First pass, the 0^th element is the pivot element.

Step 2 : Obtain the proper position of the pivot we traverse the list in both the directions using the indices how and high respectively. We initialize low to that index which is one more than index of the pivot element (1^st position)

Step 3 : The index low is incremented till we get an element at the low^th  position greater than pivot element.

Step 4 : Initialize High to n-1 and go on decrementing high till we get an element having the value less than the pivot element.

Step 5 : Check whether low and high have crossed each other. Incrementing low and decrementing high till low and high cross each other.

Step 6 : low and high cross each other, Interchange the pivot element and element at high position and find that the elements to the left of pivot element are less than it and the elements to its right are greater than it.

Step 7 : Repeat.

Step 8 : Stop

 

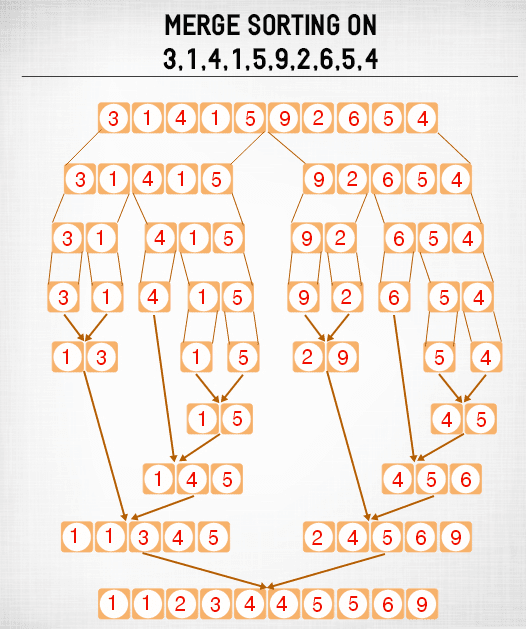
Merge Sort :

1. The basic concept of merge sort is divide the list into smaller sub lists of approximately equal size.
2. Recursively repeat this procedure till only one element is left in the sub list. After this, various sorted sub lists are merged to form sorted parent list. This process gore on recursively till the original sorted list arrived.

Algorithm :

Step 1 : If p<r

Step 2 :  Than q = [(p+r)/2];

Step 3 : Merge(A,P,Q);

Step 4 : Merge (A,Q+1,R);

Step 5 : Merge (A,P,Q,R);

Step 6 : Stop.

 

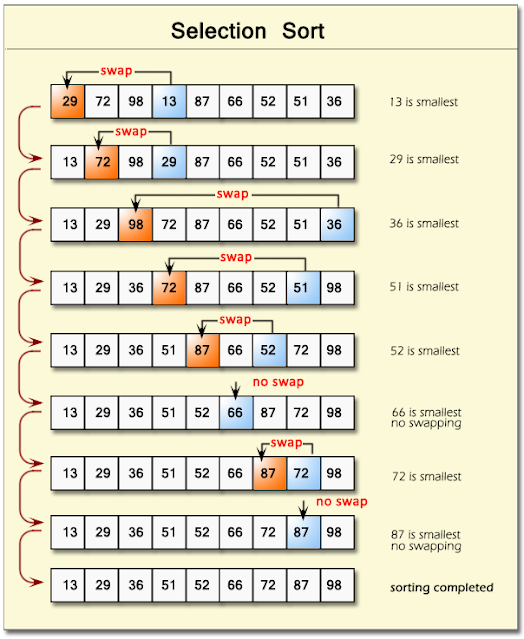
Selection Sort :

1. This sorting algorithm, iterates through the array and finds the smaller number the array and swaps it with the first element if it is smaller than the first element Next, it goes on to the second element and so on until all elements are sorted.
2. Assume the list containing  n elements. The first elements is compare with the remaining (n-1) elements.
3. The first elements is compare with the remaining (n-1) elements. The smallest element is placed at the first location.
4. Again, the second element is compare with remaining (n-2) elements, If the element found is lesser than the second element than the swap operation Is down. In this way, the entire array is checked for the smallest element and then swap.

Algorithm :

Step 1 : Set min to the first location

Step 2 : Search the min element in the array

Step 3 : Swap the first location with the minimum value in the array

Step 4 : Assign the second element as min.

Step 5 : Repeat the process until we get a sorted array.